Chapter 2 Data understanding

In Data Understanding, you will learn how to:

  • Import data
  • Get an overview about the data structure
  • Split data into training and test set using stratified sampling
  • Discover and visualize the data to gain insights

2.1 Imort Data

First of all, let’s import the data:

LINK <- "https://raw.githubusercontent.com/kirenz/datasets/master/housing.csv"
housing_df <- read_csv(LINK)

2.2 Data overview

Next, we take a look at the data structure:

California census top 4 rows of the DataFrame:

head(housing_df, 4)
## # A tibble: 4 x 10
##   longitude latitude housing_median_… total_rooms total_bedrooms population
##       <dbl>    <dbl>            <dbl>       <dbl>          <dbl>      <dbl>
## 1     -122.     37.9               41         880            129        322
## 2     -122.     37.9               21        7099           1106       2401
## 3     -122.     37.8               52        1467            190        496
## 4     -122.     37.8               52        1274            235        558
## # … with 4 more variables: households <dbl>, median_income <dbl>,
## #   median_house_value <dbl>, ocean_proximity <chr>

Data info:

glimpse(housing_df)
## Rows: 20,640
## Columns: 10
## $ longitude          <dbl> -122.23, -122.22, -122.24, -122.25, -122.25, -122.…
## $ latitude           <dbl> 37.88, 37.86, 37.85, 37.85, 37.85, 37.85, 37.84, 3…
## $ housing_median_age <dbl> 41, 21, 52, 52, 52, 52, 52, 52, 42, 52, 52, 52, 52…
## $ total_rooms        <dbl> 880, 7099, 1467, 1274, 1627, 919, 2535, 3104, 2555…
## $ total_bedrooms     <dbl> 129, 1106, 190, 235, 280, 213, 489, 687, 665, 707,…
## $ population         <dbl> 322, 2401, 496, 558, 565, 413, 1094, 1157, 1206, 1…
## $ households         <dbl> 126, 1138, 177, 219, 259, 193, 514, 647, 595, 714,…
## $ median_income      <dbl> 8.3252, 8.3014, 7.2574, 5.6431, 3.8462, 4.0368, 3.…
## $ median_house_value <dbl> 452600, 358500, 352100, 341300, 342200, 269700, 29…
## $ ocean_proximity    <chr> "NEAR BAY", "NEAR BAY", "NEAR BAY", "NEAR BAY", "N…

Data summary of numerical and categorical attributes using a function from the package skimr:

skim(housing_df)
Table 2.1: Data summary
Name housing_df
Number of rows 20640
Number of columns 10
_______________________
Column type frequency:
character 1
numeric 9
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
ocean_proximity 0 1 6 10 0 5 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
longitude 0 1.00 -119.57 2.00 -124.35 -121.80 -118.49 -118.01 -114.31 ▂▆▃▇▁
latitude 0 1.00 35.63 2.14 32.54 33.93 34.26 37.71 41.95 ▇▁▅▂▁
housing_median_age 0 1.00 28.64 12.59 1.00 18.00 29.00 37.00 52.00 ▃▇▇▇▅
total_rooms 0 1.00 2635.76 2181.62 2.00 1447.75 2127.00 3148.00 39320.00 ▇▁▁▁▁
total_bedrooms 207 0.99 537.87 421.39 1.00 296.00 435.00 647.00 6445.00 ▇▁▁▁▁
population 0 1.00 1425.48 1132.46 3.00 787.00 1166.00 1725.00 35682.00 ▇▁▁▁▁
households 0 1.00 499.54 382.33 1.00 280.00 409.00 605.00 6082.00 ▇▁▁▁▁
median_income 0 1.00 3.87 1.90 0.50 2.56 3.53 4.74 15.00 ▇▇▁▁▁
median_house_value 0 1.00 206855.82 115395.62 14999.00 119600.00 179700.00 264725.00 500001.00 ▅▇▅▂▂

Count levels of our categorical variable:

housing_df %>% 
  count(ocean_proximity,
        sort = TRUE)
## # A tibble: 5 x 2
##   ocean_proximity     n
##   <chr>           <int>
## 1 <1H OCEAN        9136
## 2 INLAND           6551
## 3 NEAR OCEAN       2658
## 4 NEAR BAY         2290
## 5 ISLAND              5

The function ggscatmat from the package GGally creates a matrix with scatterplots, densities and correlations for numeric columns. In our code, we enter the dataset housing_df, choose columns 6 to 9, a color column for our categorical variable ocean_proximity, and an alpha level of 0.8 (for transparency).

ggscatmat(housing_df, columns = 6:9, color="ocean_proximity", alpha=0.8)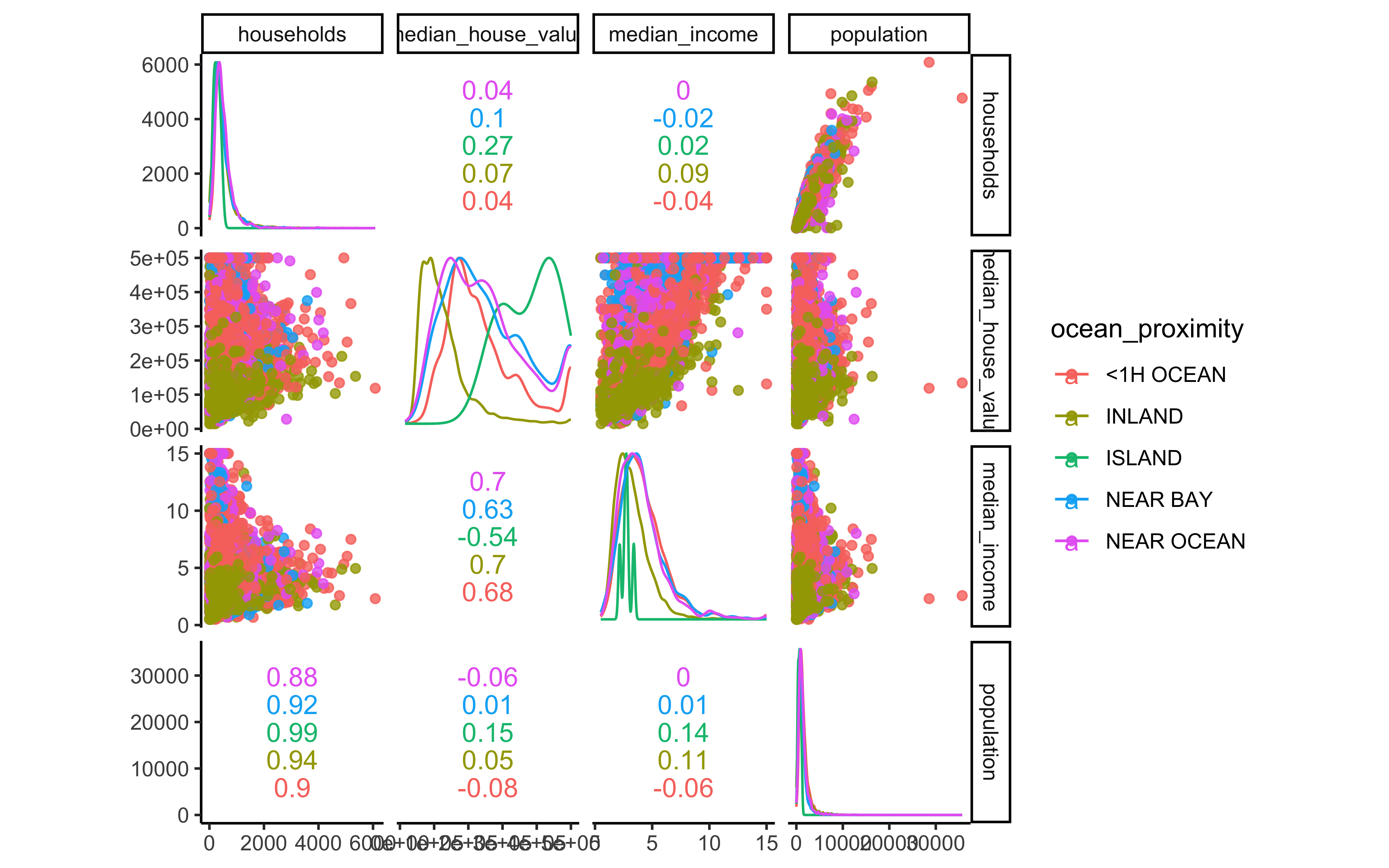

To obtain an overview of even more visualizations, we can use the function ggpairs:

ggpairs(housing_df)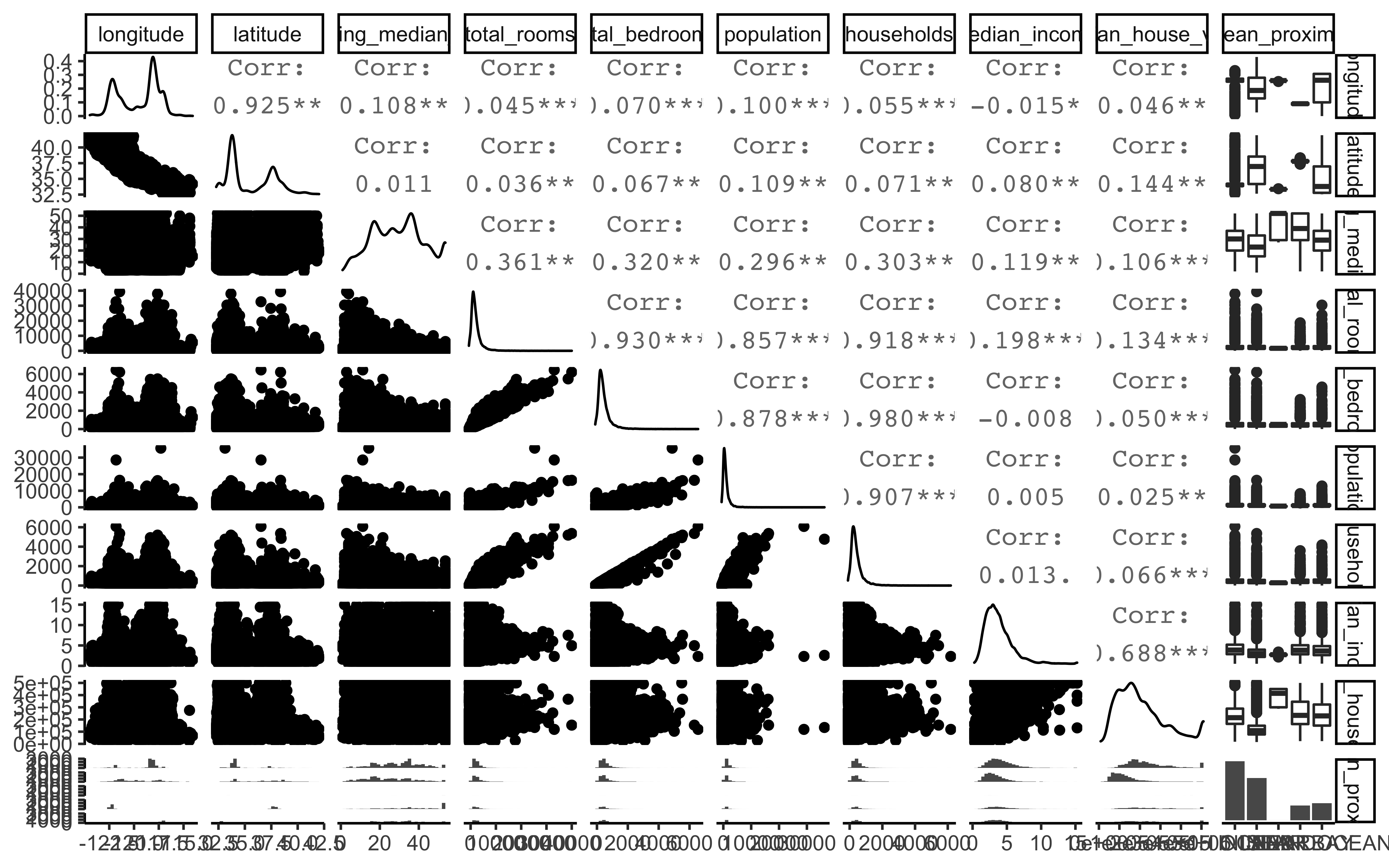

2.3 Data splitting

Let’s assume we would know that the median income is a very important attribute to predict median housing prices. Therefore, we would want to create a training and test set using stratified sampling.

A stratum (plural strata) refers to a subset (part) of the population (entire collection of items under consideration) which is being sampled. Take a look at 2.1

housing_df %>% 
  ggplot(aes(median_income)) +
  geom_histogram(bins = 30)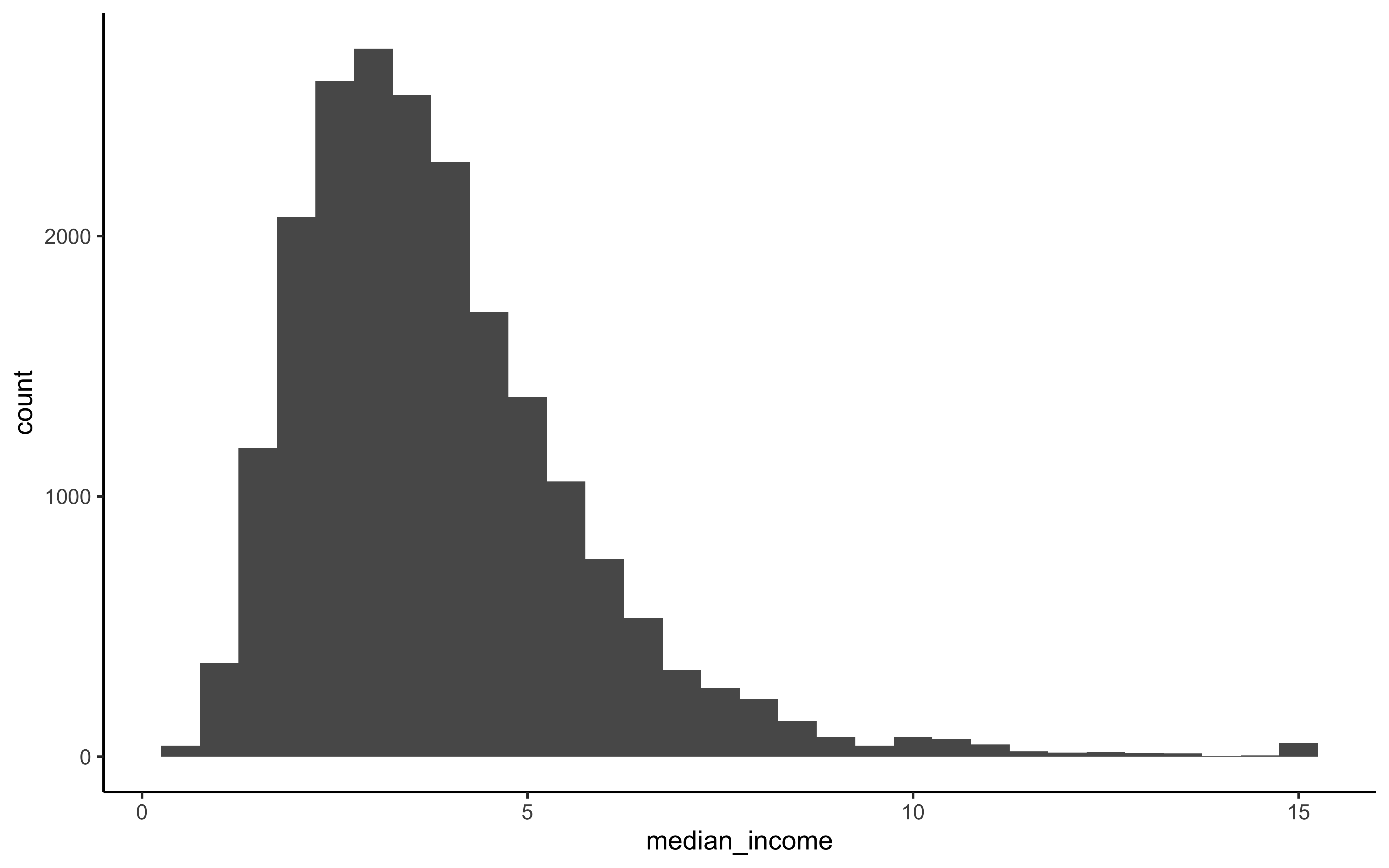
Histogram of Median Income

Figure 2.1: Histogram of Median Income

We want to ensure that the test set is representative of the various categories of incomes in the whole dataset. In other words, we would like to have instances for each stratum, or else the estimate of a stratum’s importance may be biased. This means that you should not have too many strata, and each stratum should be large enough. We use 5 strata in our example.

set.seed(42)

new_split <- initial_split(housing_df, 
                           prop = 3/4, 
                           strata = median_income, 
                           breaks = 5)

new_train <- training(new_split) 
new_test <- testing(new_split)

2.4 Data exploration

A Geographical scatterplot of the data:

housing_df %>% 
  ggplot(aes(x = longitude, y = latitude)) +
  geom_point(color = "cornflowerblue")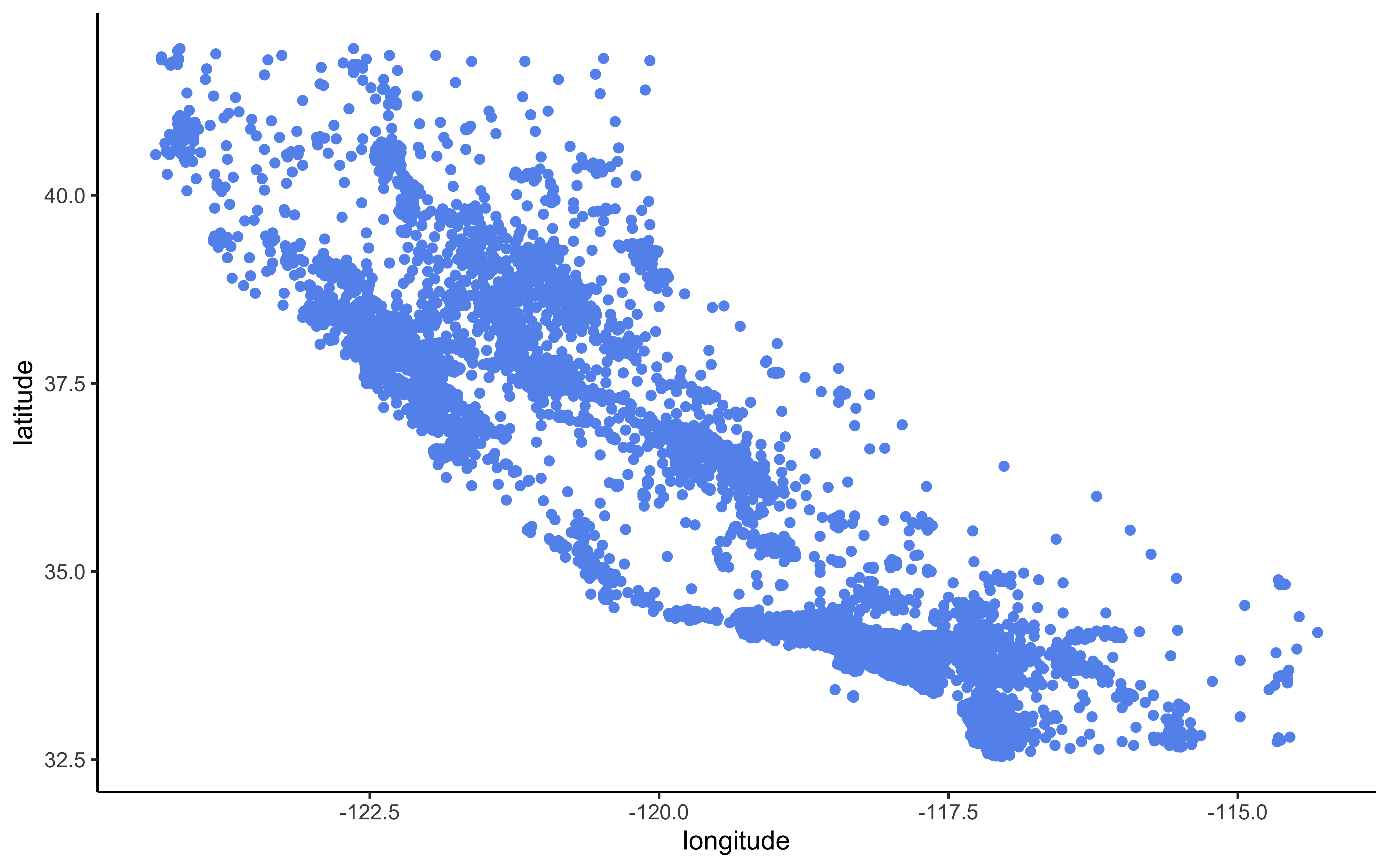
Scatterplot of longitude and latitude

Figure 2.2: Scatterplot of longitude and latitude

A better visualization that highlights high-density areas:

housing_df %>% 
  ggplot(aes(x = longitude, y = latitude)) +
  geom_point(color = "cornflowerblue", alpha = 0.1)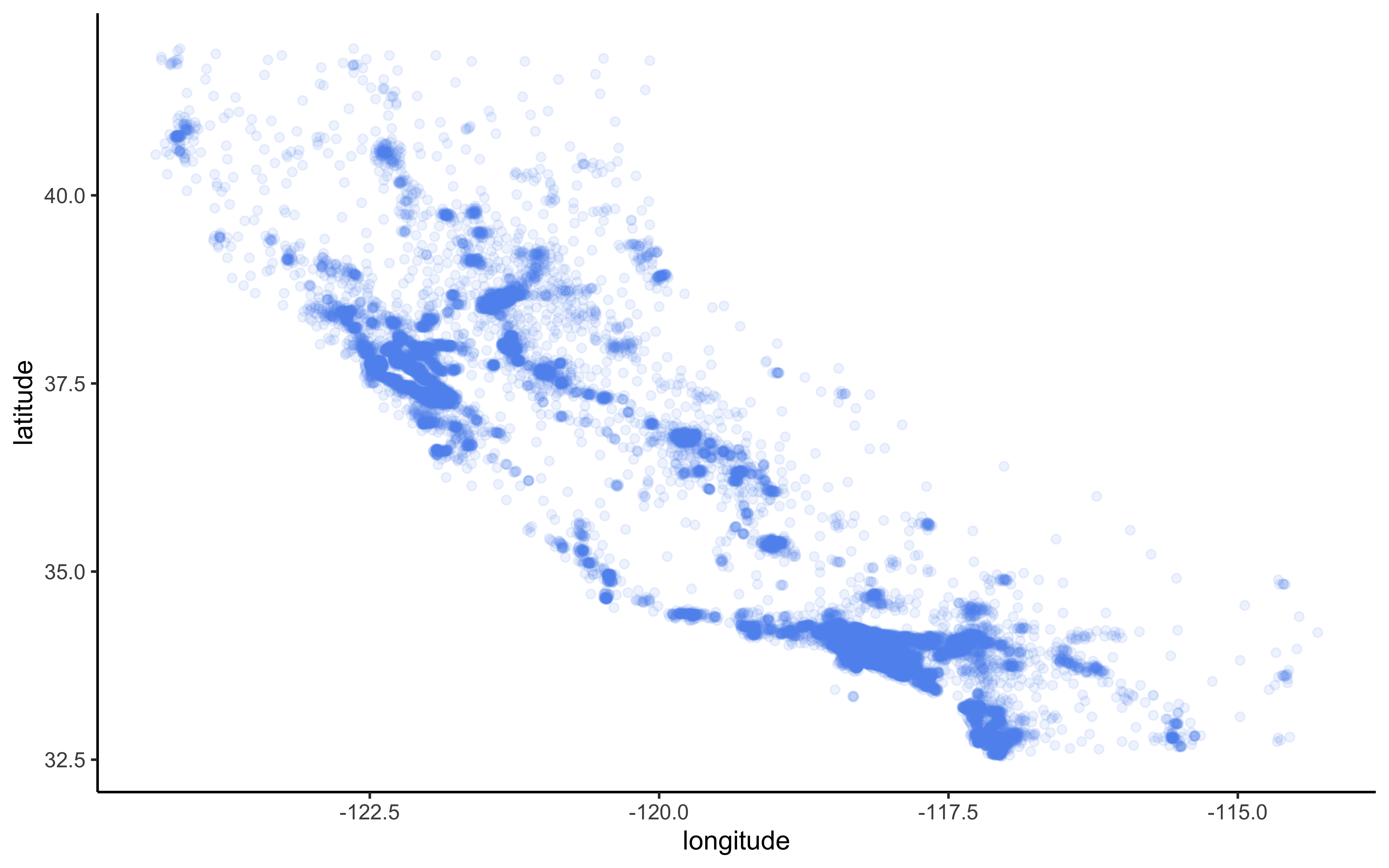
Scatterplot of longitude and latitude that highlights high-density areas

Figure 2.3: Scatterplot of longitude and latitude that highlights high-density areas

California housing prices:

  • red is expensive,
  • purple is cheap and
  • larger circles indicate areas with a larger population.
housing_df %>% 
  ggplot(aes(x = longitude, y = latitude)) +
  geom_point(aes(size = population, color = median_house_value), 
             alpha = 0.4) +
  scale_colour_gradientn(colours=rev(rainbow(4)))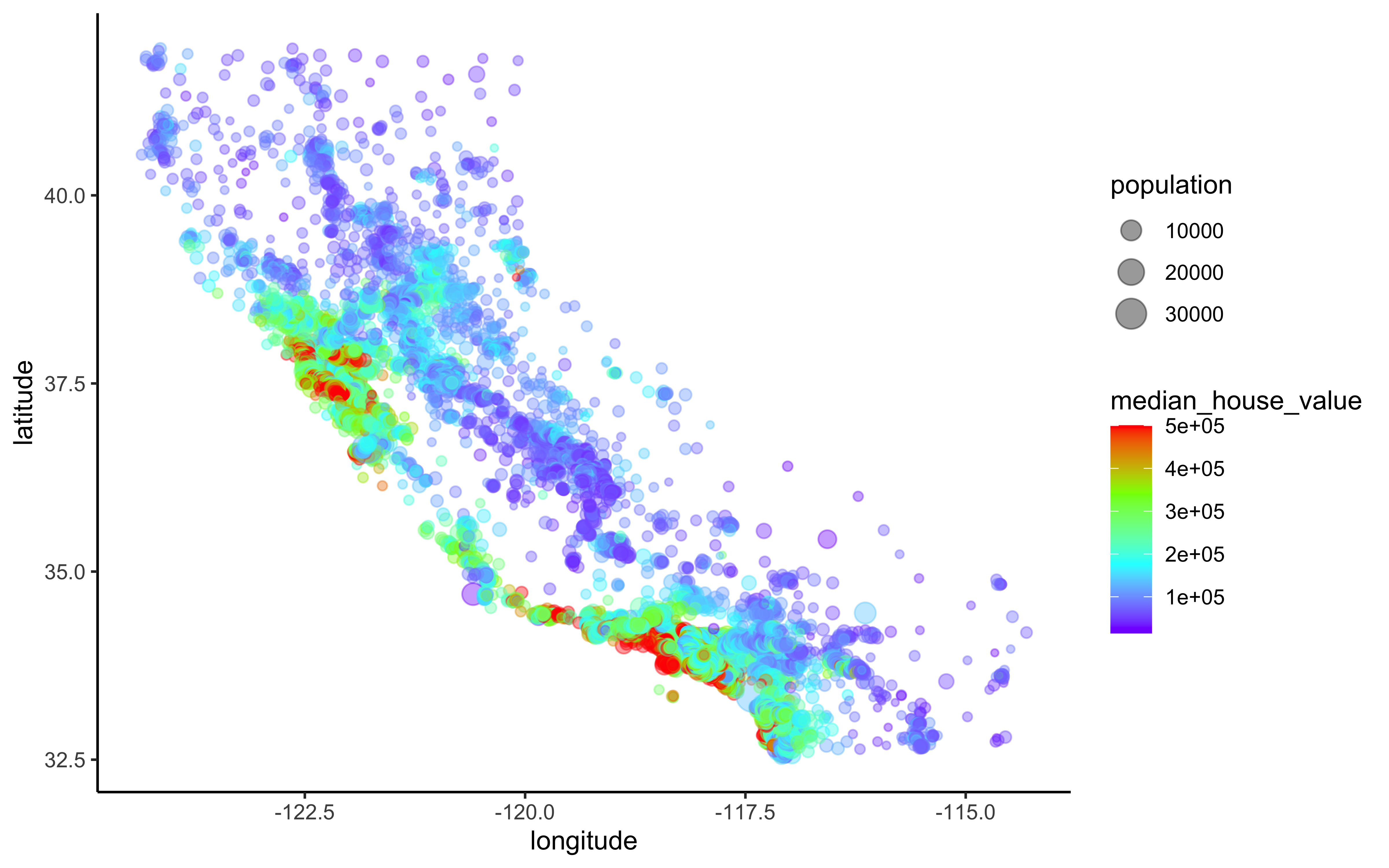
California housing_df prices

Figure 2.4: California housing_df prices 

library(ggmap)

qmplot(x = longitude, 
       y = latitude, 
       data = housing_df, 
       geom = "point", 
       color = median_house_value, 
       size = population,
       alpha = 0.4) +
  scale_colour_gradientn(colours=rev(rainbow(4)))