Online ads#

In this problem set we analyse the relationship between online ads and purchase behavior. In particular, we want to classify which online users are likely to purchase a certain product after being exposed to an online ad.

Data preparation#

import pandas as pd

df = pd.read_csv("https://raw.githubusercontent.com/kirenz/datasets/master/purchase.csv")
df
Unnamed: 0 User ID Gender Age EstimatedSalary Purchased
0 1 15624510 Male 19 19000 0
1 2 15810944 Male 35 20000 0
2 3 15668575 Female 26 43000 0
3 4 15603246 Female 27 57000 0
4 5 15804002 Male 19 76000 0
... ... ... ... ... ... ...
395 396 15691863 Female 46 41000 1
396 397 15706071 Male 51 23000 1
397 398 15654296 Female 50 20000 1
398 399 15755018 Male 36 33000 0
399 400 15594041 Female 49 36000 1

400 rows × 6 columns

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 400 entries, 0 to 399
Data columns (total 6 columns):
 #   Column           Non-Null Count  Dtype 
---  ------           --------------  ----- 
 0   Unnamed: 0       400 non-null    int64 
 1   User ID          400 non-null    int64 
 2   Gender           400 non-null    object
 3   Age              400 non-null    int64 
 4   EstimatedSalary  400 non-null    int64 
 5   Purchased        400 non-null    int64 
dtypes: int64(5), object(1)
memory usage: 18.9+ KB

# make dummy variable
df['male'] = pd.get_dummies(df['Gender'], drop_first = True)
# drop irrelevant columns
df.drop(columns= ['Unnamed: 0', 'User ID', 'Gender'], inplace = True)

# inspect outcome variable
df['Purchased'].value_counts()

0    257
1    143
Name: Purchased, dtype: int64

# prepara data for scikit learn 
X = df.drop(columns=['Purchased'])
y = df.Purchased

# make data split
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state = 123)

# create new training dataset for data exploration
train_dataset = pd.DataFrame(X_train).copy()
train_dataset['Purchased'] = pd.DataFrame(y_train)

train_dataset
Age EstimatedSalary male Purchased
177 25 22000 1 0
105 21 72000 1 0
5 27 58000 1 0
288 41 79000 1 0
279 50 36000 0 1
... ... ... ... ...
230 35 147000 0 1
98 35 73000 1 0
322 41 52000 1 0
382 44 139000 0 1
365 59 29000 0 1

280 rows × 4 columns

Exploratory data analysis (EDA)#

train_dataset.groupby(by=['Purchased']).describe().T
Purchased 0 1
Age count 180.000000 100.000000
mean 32.672222 46.090000
std 8.176018 8.589511
min 18.000000 27.000000
25% 26.000000 39.000000
50% 33.500000 47.000000
75% 39.000000 53.000000
max 59.000000 60.000000
EstimatedSalary count 180.000000 100.000000
mean 59788.888889 85460.000000
std 22884.697356 41858.207020
min 15000.000000 20000.000000
25% 46500.000000 38750.000000
50% 60000.000000 92000.000000
75% 76250.000000 122000.000000
max 134000.000000 150000.000000
male count 180.000000 100.000000
mean 0.527778 0.420000
std 0.500620 0.496045
min 0.000000 0.000000
25% 0.000000 0.000000
50% 1.000000 0.000000
75% 1.000000 1.000000
max 1.000000 1.000000

Purchasers are (on average) _______ and earn a __________ estimated salary than non-purchasers.

Visualization of differences:

import seaborn as sns

sns.pairplot(hue='Purchased', kind="reg", diag_kind="kde", data=train_dataset);
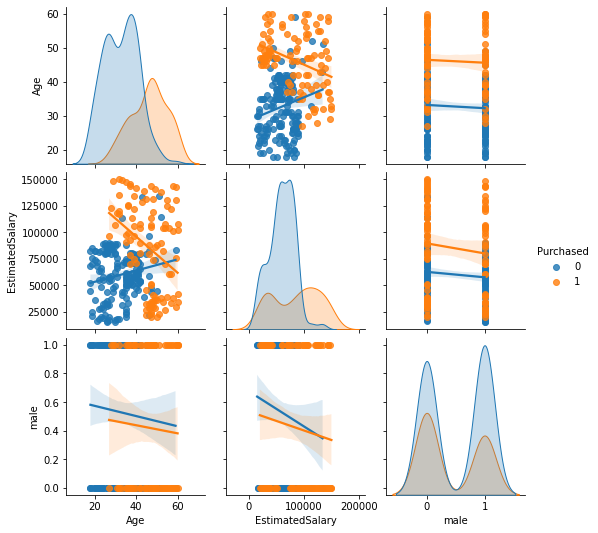
../_images/logistic-online_12_0.png

Inspect (linear) relationships between variables with correlation (pearson’s correlation coefficient)

df.corr().round(2)
Age EstimatedSalary Purchased male
Age 1.00 0.16 0.62 -0.07
EstimatedSalary 0.16 1.00 0.36 -0.06
Purchased 0.62 0.36 1.00 -0.04
male -0.07 -0.06 -0.04 1.00 
sns.kdeplot(hue="Purchased", x='Age', data=train_dataset);
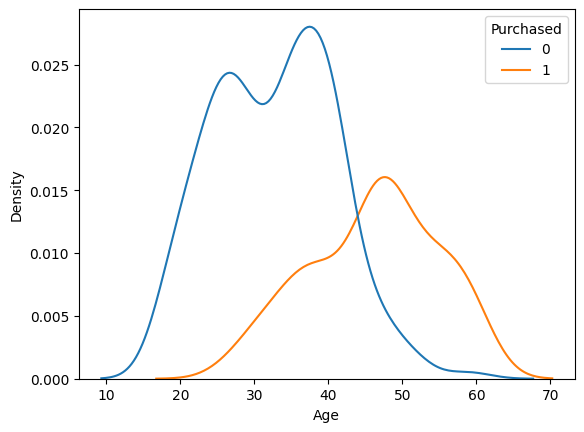
../_images/logistic-online_15_0.png

Purchasers seem to be _________ than non-purchaser.

sns.boxplot(x="male", y="Age", hue="Purchased", data=train_dataset);
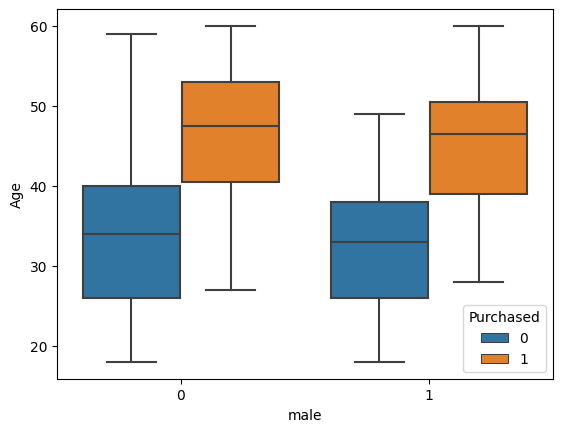
../_images/logistic-online_17_0.png

There are __________ differences regarding gender.

sns.kdeplot(hue="Purchased", x='EstimatedSalary', data=train_dataset);
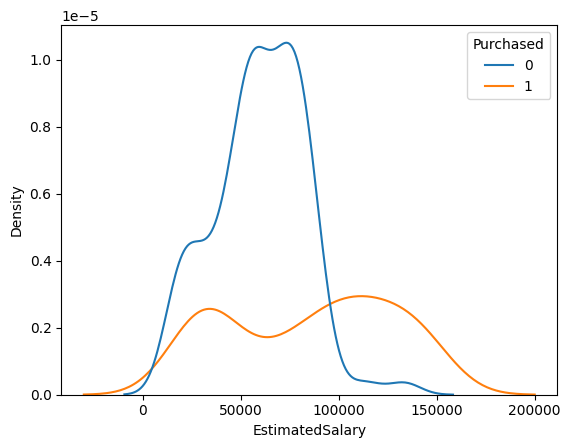
../_images/logistic-online_19_0.png

Purchaser earn a ______________ estimated salary.

sns.boxplot(x="male", y="EstimatedSalary", hue="Purchased", data=train_dataset);
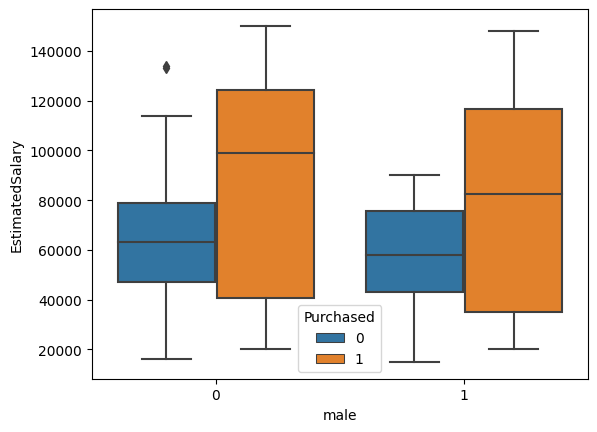
../_images/logistic-online_21_0.png

Insight: there are ___________ differences between males and females (regarding purchase behavior, age and estimated salary)

Model#

Next, we will fit a logistic regression model. In particular, we use a model that has built-in cross-validation capabilities to automatically select the best hyper-parameter for our model.

We only use our most promising predictor variables Age and EstimatedSalary for our model.

# only use meaningful predictors
features_model = ['Age', 'EstimatedSalary']

X_train = X_train[features_model] 
X_test = X_test[features_model]

from sklearn.linear_model import LogisticRegressionCV

# model
clf = LogisticRegressionCV()

# fit model to data
clf.fit(X_train, y_train)

# prediction
y_pred = clf.predict(X_test)

Classification metrics#

# Return the mean accuracy on the given test data and labels:
clf.score(X_test, y_test)

0.825

from sklearn.metrics import ConfusionMatrixDisplay

ConfusionMatrixDisplay.from_estimator(clf, X_test, y_test);
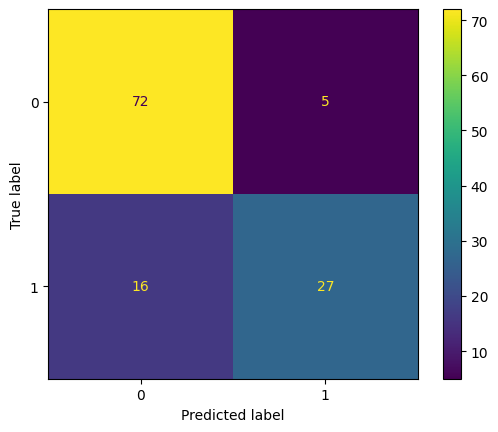
../_images/logistic-online_28_0.png 
from sklearn.metrics import classification_report

print(classification_report(y_test, y_pred, target_names=['Not purchased', 'Purchased']))

               precision    recall  f1-score   support

Not purchased       0.82      0.94      0.87        77
    Purchased       0.84      0.63      0.72        43

     accuracy                           0.82       120
    macro avg       0.83      0.78      0.80       120
 weighted avg       0.83      0.82      0.82       120

macro: Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.

weighted: Calculate metrics for each label, and find their average weighted by support (the number of true instances for each label). This alters ‘macro’ to account for label imbalance.

Note that recall is also sometimes called sensitivity or true positive rate.

  • High scores for both precision and recall show that the classifier is returning accurate results (high precision), as well as returning a majority of all positive results (high recall).

  • The importance of precision vs recall depends on the use case at hand (and the costs associated with missclassification).

  • A system with high recall but low precision returns many results, but most of its predicted labels are incorrect when compared to the training labels.

  • A system with high precision but low recall is just the opposite, returning very few results, but most of its predicted labels are correct when compared to the training labels.

  • An ideal system with high precision and high recall will return many results, with most results labeled correctly.

The unweighted recall of our model is _____

The unweighted precision of our model is _____

ROC Curve#

from sklearn.metrics import RocCurveDisplay

RocCurveDisplay.from_estimator(clf, X_test, y_test) 

<sklearn.metrics._plot.roc_curve.RocCurveDisplay at 0x7f2e602a5e50>
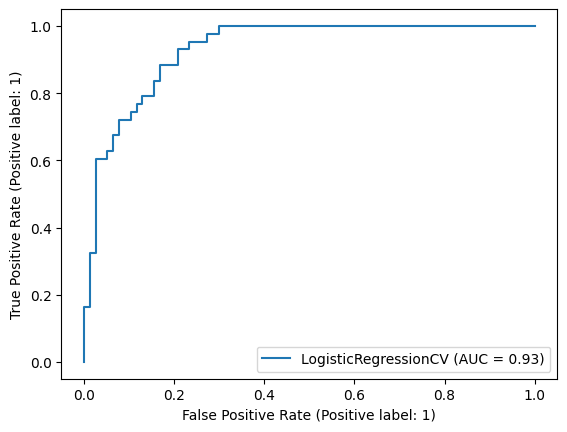
../_images/logistic-online_34_1.png

AUC Score#

from sklearn.metrics import roc_auc_score

y_score = clf.predict_proba(X_test)[:, 1]
roc_auc_score(y_test, y_score)

0.9311386288130474